Le neurone formel

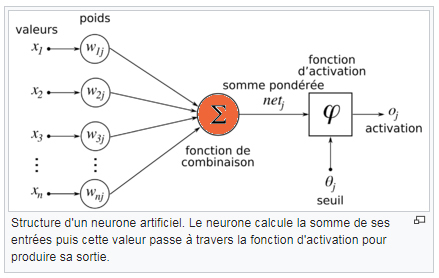
Un neurone formel est une représentation mathématique et informatique d'un neurone biologique. Le neurone formel possède généralement plusieurs entrées et une sortie qui correspondent respectivement aux dendrites et au cône d'émergence du neurone biologique (point de départ de l'axone). Les actions excitatrices et inhibitrices des synapses sont représentées, la plupart du temps, par des coefficients numériques (les poids synaptiques) associés aux entrées.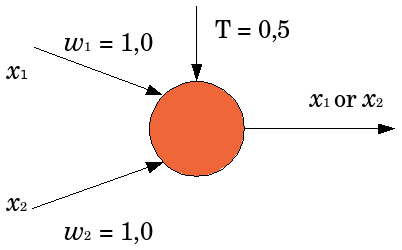

Les valeurs numériques de ces coefficients sont ajustées dans une phase d'apprentissage. Dans sa version la plus simple, un neurone formel calcule la somme pondérée des entrées reçues, puis applique à cette valeur une fonction d'activation, généralement non linéaire. La valeur finale obtenue est la sortie du neurone.

Le neurone formel est l'unité élémentaire des réseaux de neurones artificiels dans lesquels il est associé à ses semblables pour calculer des fonctions arbitrairement complexes, utilisées pour diverses applications en intelligence artificielle.

Mathématiquement, le neurone formel est une fonction à plusieurs variables et à valeurs réelles.

Formulation mathématique

On considère le cas général d'un neurone formel à m entrées, auquel on doit donc soumettre les m grandeurs numériques (ou signaux, ou encore stimuli) notées x1 à xm Un modèle de neurone formel est une règle de calcul qui permet d'associer aux m entrées une sortie : c'est donc une fonction à m variables et à valeurs réelles. Dans le modèle de McCulloch et Pitts, à chaque entrée est associé un poids synaptique, c'est-à-dire une valeur numérique notée de w1 pour l'entrée 1 jusqu'à wm pour l'entrée m.

La première opération réalisée par le neurone formel consiste en une somme des grandeurs reçues en entrées, pondérées par les coefficients synaptiques, c'est-à-dire la somme
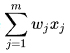
à cette grandeur s'ajoute un seuil w₀. Le résultat est alors transformé par une fonction d'activation non linéaire (parfois appelée fonction de sortie), φ.
La sortie associée aux entrées x₁ à w_m est ainsi donnée par 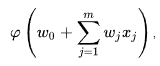qu'on peut écrire plus simplement : 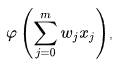en ajoutant au neurone une entrée fictive x₀ fixée à la valeur 1.

Dans la formulation d'origine de McCulloch et Pitts, la fonction d'activation est la fonction de Heaviside (fonction en marche d'escalier),
dont la valeur est 0 ou 1. Dans ce cas, on préfère parfois définir la sortie par la formule suivante
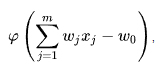qui justifie le nom de seuil donné à la valeur w₀. En effet, si la somme 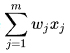dépasse w₀ la sortie du neurone est 1, alors qu'elle vaut 0 dans le cas contraire : w₀ est donc le seuil d'activation du neurone, si on considère que la sortie 0 correspond à un neurone "éteint".