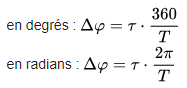Scrolling sinusoïdale
Un signal sinusoïdal est un signal (onde) dont l'amplitude, observée à un endroit précis,
est une fonction sinusoïdale du temps.
- La fonction sinus est une fonction qui permet de calculer le sinus d'un angle à partir de la valeur de cet angle.
- Une sinusoïde est la forme que prend cette fonction
L'amplitude du signal peut correspondre à une pression (son), à un déplacement (corde qui vibre),
à une quantité d'électrons en déplacement (courant électrique) ou encore à une onde électromagnétique.
|
|
|
L'importance des signaux sinusoïdaux est encore accrue par les résultats issus de l'analyse harmonique,
qui exploite le fait que toute grandeur périodique peut se décomposer en somme de termes sinusoïdaux à l'aide
de la décomposition en séries de Fourier.
Caractéristiques d'un signal sinusoïdal
Un signal sinusoïdal est caractérisé par son amplitude maximale et sa fréquence.
Il peut s'écrire sous la forme :
s(t) = A sin(ωt + φ) avec :
A : amplitude de la grandeur, appelée aussi valeur de crête, dans l'unité de la grandeur mesurée
ω : pulsation de la grandeur en rad s
-1
ω t + φ : phase instantanée en rad
φ : phase à l'origine en rad (souvent fixée par l'expérimentateur)
La pulsation, la fréquence et la période sont liés par les relations :
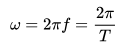
Lorsque l'on compare deux signaux de même fréquence, il est nécessaire d'indiquer de combien de temps ils sont décalés.
Les signaux sont "en phase" s'ils sont superposés, sinon il y a un déphasage.
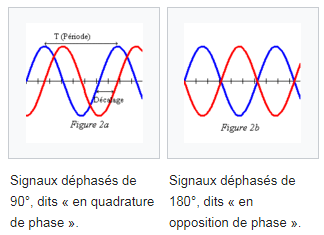
Le déphasage se déduit par une simple règle de 3 du décalage temporel séparant les deux signaux.
En effet, 0° (ou 0 radian) correspond à 0 seconde de déphasage et 360° (ou 2π radians) correspondent à des
signaux décalés d'une période (T), ils sont alors à nouveau en phase.
Si on appelle τ le décalage temporel entre les signaux, on peut écrire :
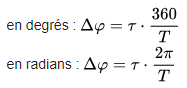

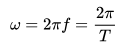 Lorsque l'on compare deux signaux de même fréquence, il est nécessaire d'indiquer de combien de temps ils sont décalés.
Les signaux sont "en phase" s'ils sont superposés, sinon il y a un déphasage.
Lorsque l'on compare deux signaux de même fréquence, il est nécessaire d'indiquer de combien de temps ils sont décalés.
Les signaux sont "en phase" s'ils sont superposés, sinon il y a un déphasage.