Algorithmes de calcul

Références

L'actualité

Parcours & Expérience





Librairie

L'information

Algorithmes de calcul > Valeur absolue d'un nombre réel

En mathématiques, la valeur absolue (parfois appelée module, c'est-à-dire mesure) d'un nombre réel est sa valeur numérique sans tenir compte de son signe. On peut la comprendre comme sa distance de zéro ; ou comme sa valeur quantitative, à laquelle le signe ajoute une idée de polarité ou de sens (comme le sens d'un vecteur).

Par exemple, la valeur absolue de -4 est 4 et celle de +4 est 4.
Pour éviter d'écrire "la valeur absolue de...", on utilise la notation |...|.
Ainsi, on écrit : |-4| = |+4| = 4

En programmation informatique, l'identificateur utilisé pour désigner la valeur absolue est usuellement abs. 

								
lire( x );
si x ≥ 0 alors écrire( '|x| =', x)
sinon écrire( '|x| =', -x)
fsi
Working progess...


Algorithmes de calcul > Résolution de l'équation du second degré dans R

En mathématiques, une équation du second degré, ou équation quadratique, est une équation polynomiale de degré 2, c'est-à-dire qu'elle peut s'écrire sous la forme : ax2 + bx + c = 0 où x est l'inconnue et les lettres a, b et c représentent les coefficients, avec a différent de 0.

Dans l'ensemble des nombres réels, une telle équation admet au maximum deux solutions, qui correspondent aux abscisses des éventuels points d'intersection de la parabole d'équation y = ax2 + bx + c avec l'axe des abscisses dans le plan muni d'un repère cartésien. La position de cette parabole par rapport à l'axe des abscisses, et donc le nombre de solutions (0, 1 ou 2) est donnée par le signe du discriminant. Ce dernier permet également d'exprimer facilement les solutions, qui sont aussi les racines de la fonction du second degré associée.

Sur le corps des nombres complexes, une équation du second degré a toujours exactement deux racines distinctes ou une racine double. Dans l'algèbre des quaternions, une équation du second degré peut avoir une infinité de solutions. 


				
début
	lire(A, B, C);
	Si A=0 alors début{A=0}
		Si B = 0 alors
			Si C = 0 alors
				écrire(R est solution)
			Sinon{C ≠ 0}
				écrire(pas de solution)
			Fsi
		Sinon {B ≠ 0}
			X1 ← C/B;
			écrire (X1)
		Fsi
	fin
	Sinon {A ≠ 0} début
		Δ ← B2 - 4*A*C ;
			Si Δ < 0 alors
				écrire(pas de solution)
			Sinon {Δ ≥ 0}
				Si Δ = 0 alors
					X1 ← -B/(2*A);
					écrire (X1)
				Sinon{Δ ≠ 0}
					X1 ← (-B + √Δ)/(2*A);
					X2 ← (-B - √Δ)/(2*A);
					écrire(X1 , X2 )
				Fsi
			Fsi
		fin
	Fsi
FinEquation
Working progess...


Algorithmes de calcul > Nombres de Armstrong

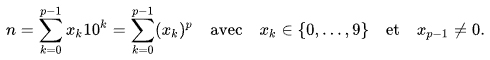
Un nombre narcissique (ou nombre d'Armstrong de première espèce, ou en anglais PPDI, pour pluperfect digit invariant) est un entier naturel n non nul qui est égal à la somme des puissances p-ièmes de ses chiffres en base dix, où p désigne le nombre de chiffres de n :

  • Tous les entiers de 1 à 9 sont narcissiques.
  • Les vingt premiers termes de la suite des 88 nombres narcissiques sont 1, 153, 370, 371, 407, 1634, 8208, 9474, 54748, 92727, 93084 et 548834.
  • 153 = 13 + 53 + 33
  • 153 = 1 + 125 + 27, est un nombre de Armstrong.

Liste complète : Il y a exactement 88 nombres narcissiques (vrais). Le plus grand a 39 chiffres. Prouvé en 1985 par D. Winter et vérifié par D. Hoey. Liste complète en 1994 par Mendes Oliveira e Silva.


Algorithmes de calcul > Nombres parfaits

En arithmétique, un nombre parfait est un entier naturel n tel que σ(n) = 2n où σ(n) est la somme des diviseurs positifs de n. Cela revient à dire qu'un entier naturel est parfait s'il est égal à la moitié de la somme de ses diviseurs ou encore à la somme de ses diviseurs stricts.

Ainsi 6 est un nombre parfait car 2 x 6 = 12 = 1 + 2 + 3 + 6, ou encore 6 = 1 + 2 + 3.

Les quatre premiers nombres parfaits sont connus depuis l'Antiquité :

  • 6 = 21(22 - 1) = (1 + 2) + 3
  • 28 = 22(23 - 1) = (1 + 2 + 4) + (7 + 14)
  • 496 = 24(25 - 1) = (1 + 2 + 4 + 8 + 16) + (31 + 62 + 124 + 248)
  • 8128 = 26(27 - 1) = (1 + 2 + 4 + 8 + 16 + 32 + 64) + (127 + 254 + 508 + 1 016 + 2 032 + 4 064).

								
Algorithme Parfait
	Entrée: n ∈ N
	Sortie: nbr ∈ N
	Local: somdiv, k, compt ∈ N

	début
		lire(n);
		compt ← 0;
		nbr ← 2;
	Tantque(compt < n) Faire
		somdiv ← 1;
		Pour k ← 2 jusquà nbr-1 Faire
			Si reste(nbr par k) = 0 Alors // k divise nbr
				somdiv ← somdiv + k
			Fsi
		Fpour ;
		Si somdiv = nbr Alors
			ecrire(nbr) ;
			compt ← compt+1;
		Fsi;
		nbr ← nbr+1
	Ftant
FinParfait
Il n'existe que huit nombres parfaits inférieurs à un mille trillions (1021)


Algorithmes de calcul > PGCD de 2 entiers (méthode Euclide)

Le PGCD de nombres entiers différents de zéro est, parmi les diviseurs communs à ces entiers, le plus grand d'entre eux. PGCD signifie plus grand commun diviseur. Par exemple, les diviseurs positifs de 30 sont, dans l'ordre : 1, 2, 3, 5, 6, 10, 15 et 30. Ceux de 18 sont 1, 2, 3, 6, 9 et 18. Les diviseurs communs de 30 et 18 étant 1, 2, 3 et 6, leur PGCD est 6. Ce qui se note : PGCD(30, 18) = 6. 

								
Algorithme Pgcd
	Entrée: a,b ∈ N* x N*
	Sortie: pgcd ∈ N
	Local: r,t ∈ N x N
		
		début
			lire(a,b);
			Si ba Alors
				t ← a ;
				a ← b ;
				b ← t
			Fsi;
			Répéter
				r ← a mod b ;
				a ← b ;
				b ← r
			jusquà r = 0;
			pgcd ← a;
			ecrire(pgcd)
FinPgcd
Working progess...


Algorithmes de calcul > PGCD de 2 entiers (méthode Egyptienne)

Le PGCD de nombres entiers différents de zéro est, parmi les diviseurs communs à ces entiers, le plus grand d'entre eux. PGCD signifie plus grand commun diviseur. Par exemple, les diviseurs positifs de 30 sont, dans l'ordre : 1, 2, 3, 5, 6, 10, 15 et 30. Ceux de 18 sont 1, 2, 3, 6, 9 et 18. Les diviseurs communs de 30 et 18 étant 1, 2, 3 et 6, leur PGCD est 6. Ce qui se note : PGCD(30, 18) = 6. 

								
Lire (p, q ) ;
	Tantque p ≠ q faire
		Si p > q alors
			p ← p - q
		sinon
			q ← q - p
		FinSi
	FinTant;
Ecrire( " PGCD = " , p )
Working progess...


Algorithmes de calcul > Nombres premiers (while et do-while)

Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs (qui sont alors 1 et lui-même). Ainsi, 1 n'est pas premier car il n'a qu'un seul diviseur entier positif ; 0 non plus car il est divisible par tous les entiers positifs. Par opposition, un produit de deux entiers strictement supérieurs à 1 est dit composé. Par exemple 6 = 2 x 3 est composé, tout comme 12 = 3 x 4 ou 2 x 6, mais 11 est premier car 1 et 11 sont les seuls diviseurs de 11.

Les nombres 0 et 1 ne sont ni premiers ni composés. Certains mathématiciens considéraient autrefois (jusqu'au 19e siècle) 1 comme un nombre premier, mais durant le début du 20e siècle, un consensus exclut définitivement sa primalité.

Les vingt-cinq nombres premiers inférieurs à 100 sont :
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 et 97.

								
Algorithme Premier
	Entrée: n ∈ N
	Sortie: nbr ∈ N
	Local:	Est_premier ∈ {Vrai , Faux}
			divis,compt ∈ N2;
	
	début
		lire(n);
		compt ← 1;
		ecrire(2);
		nbr ← 3;
		Tantque(compt < n) Faire
			divis ← 3;
			Est_premier ← Vrai;
			Répéter
				Si reste(nbr par divis) = 0 Alors
				Est_premier ← Faux
			Sinon
				divis ← divis+2
			Fsi
		jusquà (divis > nbr / 2) ou (Est_premier=Faux);
		Si Est_premier = Vrai Alors
			ecrire(nbr);
			compt ← compt+1
		Fsi;
		nbr ← nbr+1
		Ftant
	FinPremier
Working progess...


Algorithmes de calcul > Nombres premiers (for)

Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs (qui sont alors 1 et lui-même). Ainsi, 1 n'est pas premier car il n'a qu'un seul diviseur entier positif ; 0 non plus car il est divisible par tous les entiers positifs. Par opposition, un produit de deux entiers strictement supérieurs à 1 est dit composé. Par exemple 6 = 2 x 3 est composé, tout comme 12 = 3 x 4 ou 2 x 6, mais 11 est premier car 1 et 11 sont les seuls diviseurs de 11.

Les nombres 0 et 1 ne sont ni premiers ni composés. Certains mathématiciens considéraient autrefois (jusqu'au 19e siècle) 1 comme un nombre premier, mais durant le début du 20e siècle, un consensus exclut définitivement sa primalité.

Les vingt-cinq nombres premiers inférieurs à 100 sont :
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 et 97.



								
Algorithme Premier
	Entrée: n ∈ N
	Sortie: nbr ∈ N
	Local:	Est_premier ∈ {Vrai , Faux}
			divis,compt ∈N2;
	
	début
		lire(n);
		compt ← 1;
		ecrire(2);
		nbr ← 3;
		Tantque(compt < n) Faire
			divis ← 3;
			Est_premier ← Vrai;
			Répéter
				Si reste(nbr par divis) = 0 Alors
					Est_premier ← Faux
				Sinon
					divis ← divis+2
				Fsi
			jusquà (divis > nbr / 2)ou (Est_premier = Faux);
				Si Est_premier =Vrai Alors
					ecrire(nbr);
					compt ← compt+1
				Fsi;
			nbr ← nbr+2 // nbr impairs
		Ftant
	FinPremier
Working progess...


Algorithmes de calcul > Nombre d'or

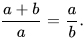
Le nombre d'or (ou section dorée, proportion dorée, ou encore divine proportion) est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b) c'est-à-dire lorsque :

Le découpage d'un segment en deux longueurs vérifiant cette propriété est appelé par Euclide découpage en "extrême et moyenne raison". Le nombre d'or est maintenant souvent désigné par la lettre φ (phi).

Ce nombre irrationnel est l'unique solution positive de l'équation x2 = x + 1. Il vaut : 

								
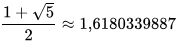
n,Un ,Un1 ,Un2 : sont des entiers naturels
Vn ,Vn1 , ε : sont des nombres réels

lire( ε ); // précision demandée
	Un2 ← 1;
	Un1 ← 2;
	Vn1 ← 2;
	n ← 2; // rang du terme courant
Itération
	n ← n + 1;
	Un ← Un1 + Un2 ;
	Vn ← Un / Un1 ;
	si |Vn - Vn1| ≤ ε alors Arrêt de la boucle ; // la précision est atteinte
	sinon
		Un2 ← Un1 ;
		Un1 ← Un ;
		Vn1 ← Vn ;
	fsi
fin Itération
ecrire (Vn , n);
On considère deux suites numériques (U) et (V) telles que pour n strictement supérieur à 2 :
Un = Un-1 + Un-2
et
Vn = Un / Un-1

On montre que la suite (V) tend vers une limite appelée nombre d'or
Nombre d'Or = 1,61803398874989484820458683436564.